شرح جميع خوارزميات التعلم الآلي

تعلم الآلة مع Scikit-Learn

Scikit-Learn هي مكتبة في بايثون توفر العديد من خوارزميات التعلم غير الخاضعة unsupervised للإشراف وخوارزميات التعلم الخاضعة للأشراف supervised. إنها مبنية على بعض التقنيات التي قد تكون على دراية بها بالفعل، مثل NumPy و pandas و Matplotlib.

تشمل الوظائف التي يوفرها موقع scikit-Learn ما يلي:

• الانحدار Regression: بما في ذلك الانحدار الخطي Linear  واللوجستي Logistic.
• التصنيف Classification: بما في ذلك K-أقرب الجيران K-Nearest Neighbors
• التجميع Clustering: بما في ذلك K-Means و K-Means++ .
• اختيار النموذج Model selection.
• المعالجة المسبقة Preprocessing: بما في ذلك التسوية Min-Max.

سأشرح في هذه المقالة جميع خوارزميات التعلم الآلي باستخدام scikit-Learn التي تحتاج إلى تعلمها كعالم بيانات.

لنبدأ باستيراد المكتبات:

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.linear_model import LinearRegression
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from scipy import stats
import pylab as pl

المخمن Estimator

بالنظر إلى كائن مخمن scikit-Learn اسمه model، تتوفر الطرق التالية:

متوفر في جميع المخمنين

model.fit() : ملاءمة (fit) بيانات التدريب. بالنسبة لتطبيقات التعلم الخاضعة للإشراف، يقبل هذا وسيطتين: البيانات X والتسميات y (على سبيل المثال، model.fit(X, y) (بالنسبة لتطبيقات التعلم غير الخاضعة للإشراف، لا يقبل هذا سوى وسيطة واحدة ، البيانات X (على سبيل المثال ، model.fit (X)).

متوفر في المخمنين الخاضع للإشراف

model.predict(): بالنظر إلى نموذج مدرب، توقع تسمية مجموعة جديدة من البيانات. تقبل هذه الطريقة وسيطة واحدة، البيانات الجديدة X_new (على سبيل المثال model.predict (X_new)) ، وترجع التسمية التي تم تعلمها لكل كائن في المصفوفة.

model.predict_proba(): بالنسبة لمشاكل التصنيف، يقدم بعض المخمنين أيضًا هذه الطريقة، والتي تُرجع احتمالية أن الملاحظة الجديدة لها كل تصنيف فئوي. في هذه الحالة، يتم إرجاع التسمية ذات أعلى احتمالية بواسطةmodel.predict(). model.score()بالنسبة لمسائل التصنيف أو الانحدار ، فإن معظم (الكل؟) المخمنون يطبقون طريقة score. تتراوح الدرجات بين 0 و 1، مع وجود درجة أكبر تشير إلى ملاءمة أفضل.

متوفر في المخمنين غير الخاضعين للاشراف

model.predict(): توقع التسميات في خوارزميات التجميع. model.transform(): في ضوء نموذج غير خاضع للإشراف ، قم بتحويل البيانات الجديدة إلى أساس جديد. يقبل هذا أيضًا وسيطة واحدة X_new، ويعيد التمثيل الجديد للبيانات بناءً على النموذج غير الخاضع للإشراف. model.fit_transform(): يقوم بعض المخمنين بتنفيذ هذه الطريقة، والتي تؤدي بكفاءة أكبر إلى ملاءمة وتحويل على نفس بيانات الإدخال.

تنزيل وقراءة مجموعة البيانات (Iris).

data =  pd.read_csv('Iris.csv')
data.head()

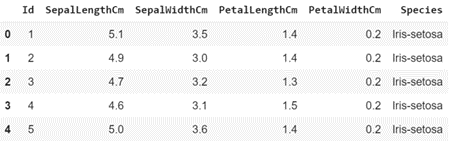
print(data.shape)

#Output
(150, 6)

data.info()

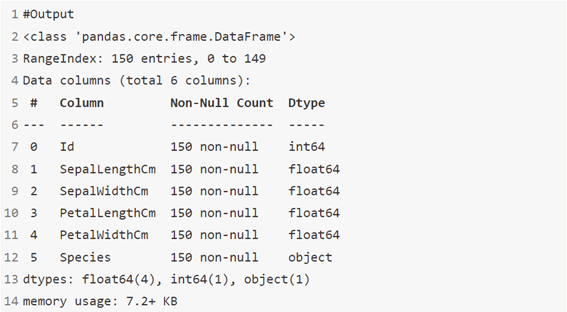
التصوير

بعض التمثيل البياني للمعلومات والبيانات.

sns.FacetGrid(data,hue='Species',size=5)\
.map(plt.scatter,'SepalLengthCm','SepalWidthCm')\
.add_legend()

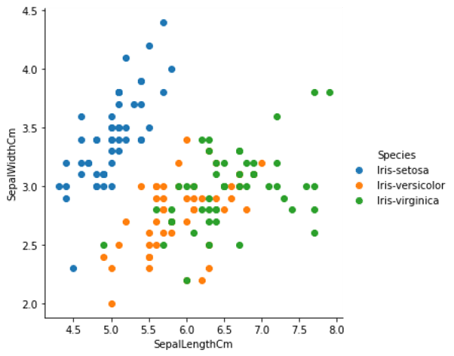
sns.pairplot(data,hue='Species')

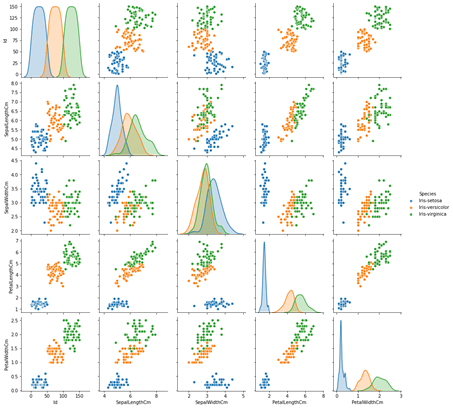
تحضير التدريب والاختبار

يوفر scikit-learn وظيفة مفيدة لتقسيم البيانات، train_test_split ، الذي يقسم بياناتك إلى مجموعة تدريب ومجموعة اختبار.

عادةً ما يكون التدريب والاختبار 70٪ للتدريب و30٪ للاختبار

• مجموعة التدريب لملاءمة (fitting) النموذج.
• مجموعة الاختبار للتقييم (evaluation) فقط.

X = data.iloc[:, :-1].values    #   X -> Feature Variables
y = data.iloc[:, -1].values #   y ->  Target
# Splitting the data into Train and Test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 0)

الخوارزمية 1: الانحدار الخطي Linear Regression

يتم استخدامه لتقدير القيم الحقيقية (تكلفة المنازل، عدد المكالمات، إجمالي المبيعات وما إلى ذلك) بناءً على المتغير (المتغيرات) المستمر. هنا، نؤسس علاقة بين المتغيرات المستقلة والتابعة من خلال ملاءمة أفضل خط fitting a best line. يُعرف هذا الخط الأكثر ملاءمة بخط الانحدار regression line ويتم تمثيله بمعادلة خطية ** Y = a * X + b.

#converting object data type into int data type using labelEncoder for Linear reagration in this case

XL = data.iloc[:, :-1].values    #   X -> Feature Variables
yL = data.iloc[:, -1].values #   y ->  Target

from sklearn.preprocessing import LabelEncoder

le = LabelEncoder()
Y_train= le.fit_transform(yL)

print(Y_train)  # this is Y_train categotical to numerical
# This is only for Linear Regretion 

X_trainL, X_testL, y_trainL, y_testL = train_test_split(XL, Y_train, test_size = 0.3, random_state = 0)

from sklearn.linear_model import LinearRegression
modelLR = LinearRegression()
modelLR.fit(X_trainL, y_trainL)
Y_pred = modelLR.predict(X_testL)

from sklearn import metrics
#calculating the residuals
print('y-intercept             :' , modelLR.intercept_)
print('beta coefficients       :' , modelLR.coef_)
print('Mean Abs Error MAE      :' ,metrics.mean_absolute_error(y_testL,Y_pred))
print('Mean Sqrt Error MSE     :' ,metrics.mean_squared_error(y_testL,Y_pred))
print('Root Mean Sqrt Error RMSE:' ,np.sqrt(metrics.mean_squared_error(y_testL,Y_pred)))
print('r2 value                :' ,metrics.r2_score(y_testL,Y_pred))

#Output
y-intercept             : -0.024298523519848292
beta coefficients       : [ 0.00680677 -0.10726764 -0.00624275  0.22428158  0.27196685]
Mean Abs Error MAE      : 0.14966835490524963
Mean Sqrt Error MSE     : 0.03255451737969812
Root Mean Sqrt Error RMSE: 0.18042870442282213
r2 value                : 0.9446026069799255

الخوارزمية 2: شجرة القرار Decision Tree

هذه إحدى الخوارزميات المفضلة لدي وأنا أستخدمها كثيرًا. إنه نوع من خوارزمية التعلم الخاضع للإشراف والتي تستخدم في الغالب لمشاكل التصنيف. والمثير للدهشة أنه يعمل مع كل من المتغيرات المعتمدة الفئوية categorical والمستمرة continuous.

في هذه الخوارزمية، قمنا بتقسيم السكان إلى مجموعتين متجانستين أو أكثر. يتم ذلك بناءً على السمات الأكثر أهمية / المتغيرات المستقلة لتكوين مجموعات متميزة قدر الإمكان.

# Decision Tree's
from sklearn.tree import DecisionTreeClassifier

Model = DecisionTreeClassifier()

Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

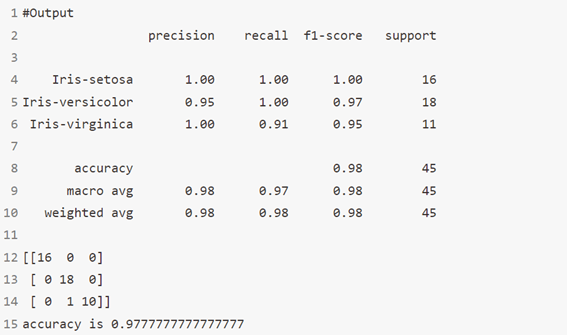
الخوارزمية 3: الغابة العشوائية RandomForest

الغامة العشوائية Random Forest هو مصطلح علامة تجارية لمجموعة من أشجار القرار. في Random Forest، لدينا مجموعة من أشجار القرار (المعروفة باسم “الغابة Forest”). لتصنيف كائن جديد بناءً على السمات، تعطي كل شجرة تصنيفًا ونقول الشجرة “أصوات votes” لتلك الفئة. تختار الغابة التصنيف الحاصل على أكبر عدد من الأصوات (على جميع الأشجار في الغابة).

from sklearn.ensemble import RandomForestClassifier
Model=RandomForestClassifier(max_depth=2)
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

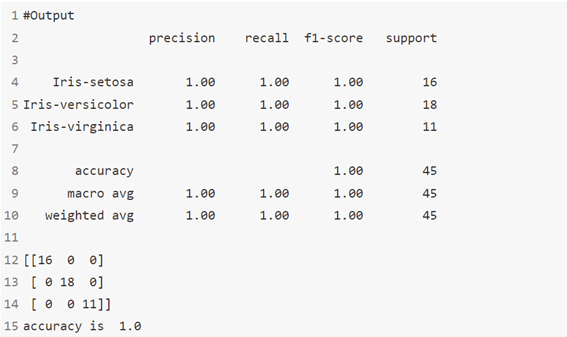
الخوارزمية 4: الانحدار اللوجستي Logistic Regression

لا ترتبك من اسمه! إنه تصنيف وليس خوارزمية انحدار. يتم استخدامه لتقدير القيم المنفصلة discrete values (القيم الثنائية مثل 0/1، نعم / لا، صواب / خطأ) بناءً على مجموعة معينة من المتغيرات المستقلة.

بكلمات بسيطة، يتنبأ باحتمالية حدوث حدث من خلال ملاءمة البيانات لوظيفة منطقية. ومن ثم، يُعرف أيضًا باسم الانحدار المنطقي logic regression. نظرًا لأنه يتوقع الاحتمال، تقع قيم مخرجاته بين 0 و1 (كما هو متوقع).

# LogisticRegression
from sklearn.linear_model import LogisticRegression
Model = LogisticRegression()
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

خوارزمية 5: K-أقرب الجيران K Nearest Neighbors

يمكن استخدامه لكل من مشاكل التصنيف والانحدار. ومع ذلك، فإنه يستخدم على نطاق واسع في مشاكل التصنيف في الصناعة. K-أقرب للجيران عبارة عن خوارزمية بسيطة تخزن جميع الحالات المتاحة وتصنف الحالات الجديدة بأغلبية أصوات جيرانها k. الحالة التي يتم تخصيصها للفئة هي الأكثر شيوعًا بين أقرب جيرانها من K مقاسة بدالة المسافة.

# K-Nearest Neighbours
from sklearn.neighbors import KNeighborsClassifier

Model = KNeighborsClassifier(n_neighbors=8)
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score

print('accuracy is',accuracy_score(y_pred,y_test))

الخوارزمية 6: نايف بايز Naive Bayes

إنها تقنية تصنيف تعتمد على نظرية بايز Bayes’ theorem مع افتراض الاستقلال بين المتنبئين. بعبارات بسيطة، يفترض مصنف Naive Bayes أن وجود ميزة معينة في فئة لا علاقة لها بوجود أي ميزة أخرى.

على سبيل المثال، يمكن اعتبار الفاكهة على أنها تفاحة إذا كانت حمراء ودائرية وقطرها حوالي 3 بوصات. حتى إذا كانت هذه الميزات تعتمد على بعضها البعض أو على وجود ميزات أخرى، فإن مصنف Naive Bayes سوف يأخذ في الاعتبار كل هذه الخصائص للمساهمة بشكل مستقل في احتمال أن تكون هذه الفاكهة تفاحة.

# Naive Bayes
from sklearn.naive_bayes import GaussianNB
Model = GaussianNB()
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

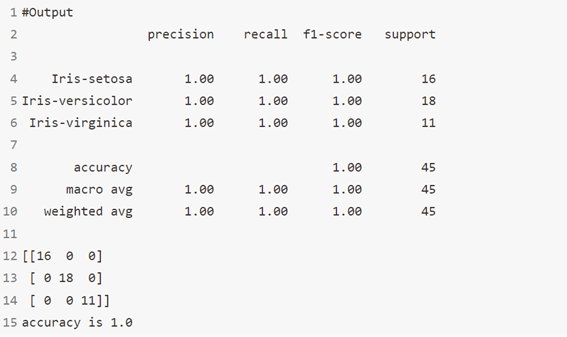
الخوارزمية 7: آلات المتجهات الداعمة Support Vector Machines

إنها طريقة تصنيف. في هذه الخوارزمية، نرسم كل عنصر بيانات كنقطة في الفضاء ذي البعد n (حيث n هو عدد الميزات التي لديك) مع قيمة كل ميزة هي قيمة إحداثيات معينة.

على سبيل المثال، إذا كان لدينا ميزتان فقط مثل الطول وطول الشعر للفرد، فسنقوم أولاً برسم هذين المتغيرين في مساحة ثنائية الأبعاد حيث تحتوي كل نقطة على إحداثيين (تُعرف هذه الإحداثيات باسم متجهات الدعم Support Vectors).

# Support Vector Machine
from sklearn.svm import SVC

Model = SVC()
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score

print('accuracy is',accuracy_score(y_pred,y_test))

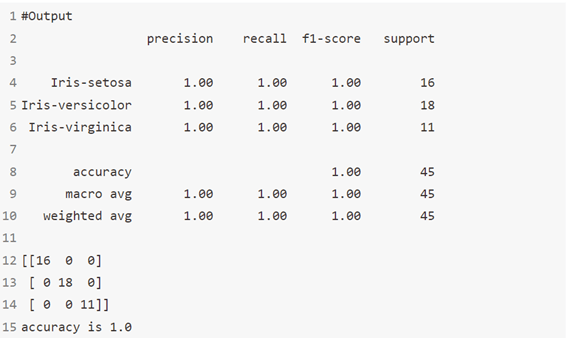
الخوارزمية 8: مصنف الجيران الشعاعي Radius Neighbors Classifier

في scikit-learn أن RadiusNeighboursClassifier مشابه جدًا لـ KNeighboursClassifier باستثناء معلمتين. أولاً، في RadiusNeighboursClassifier ، نحتاج إلى تحديد نصف قطر المنطقة الثابتة المستخدمة لتحديد ما إذا كانت الملاحظة مجاورة باستخدام نصف القطر.

ما لم يكن هناك سبب موضوعي لتعيين نصف القطر على قيمة معينة، فمن الأفضل معاملته مثل أي معلمة فائقة أخرى وضبطها أثناء اختيار النموذج. المعلمة الثانية المفيدة هي outlier_label، والتي تشير إلى التسمية التي تعطي ملاحظة لا تحتوي على ملاحظات داخل نصف القطر – والتي يمكن أن تكون في حد ذاتها أداة مفيدة في كثير من الأحيان لتحديد القيم المتطرفة outliers.

#Output
from sklearn.neighbors import  RadiusNeighborsClassifier
Model=RadiusNeighborsClassifier(radius=8.0)
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

#summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_test,y_pred))

#Accouracy score
print('accuracy is ', accuracy_score(y_test,y_pred))

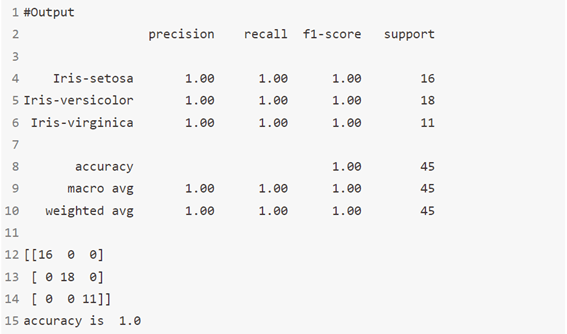
الخوارزمية 9: المصنف العدواني السلبي Passive Aggressive Classifier

خوارزمية PA هي خوارزمية تعلم عبر الإنترنت تعتمد على الهامش للتصنيف الثنائي. على عكس خوارزمية PA، وهي طريقة تعتمد على الهامش الثابت، فإن خوارزمية PA-I هي طريقة تعتمد على الهامش الناعم وقوة للضوضاء.

from sklearn.linear_model import PassiveAggressiveClassifier
Model = PassiveAggressiveClassifier()
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

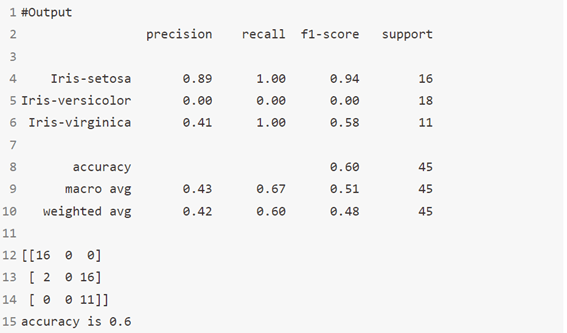
خوارزمية 10: BernoulliNB

مثل MultinomialNB ، هذا المصنف مناسب للبيانات المنفصلة discrete data. الفرق هو أنه بينما يعمل MultinomialNB مع أعداد التكرار occurrence counts، تم تصميم BernoulliNB للميزات الثنائية / المنطقية.

# BernoulliNB
from sklearn.naive_bayes import BernoulliNB
Model = BernoulliNB()
Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

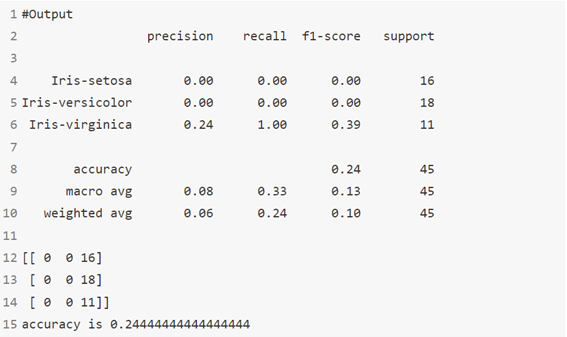
الخوارزمية 11: ExtraTreeClassifier

ExtraTreesClassifier هي طريقة تعلم جماعية ensemble learning تعتمد أساسًا على أشجار القرار. يقوم ExtraTreesClassifier ، مثل RandomForest ، بعمل عشوائي لقرارات معينة ومجموعات فرعية من البيانات لتقليل الإفراط في التعلم من البيانات ,والضبط الزائد overfitting. دعونا نلقي نظرة على بعض الطرق الجماعية مرتبة من التباين العالي إلى التباين المنخفض ، المنتهية في ExtraTreesClassifier.

# ExtraTreeClassifier
from sklearn.tree import ExtraTreeClassifier

Model = ExtraTreeClassifier()

Model.fit(X_train, y_train)

y_pred = Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))

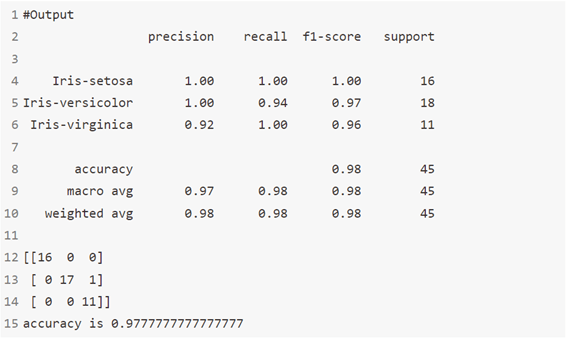
خوارزمية 12: مصنف التعبئة Bagging classifier

مُصنِّف التعبئة عبارة عن meta-estimator جماعي يلائم المصنفات الأساسية كل منها في مجموعات فرعية عشوائية من مجموعة البيانات الأصلية ثم تجميع تنبؤاتها الفردية (إما عن طريق التصويت أو عن طريق المتوسط) لتشكيل توقع نهائي. يمكن استخدام مثل هذا meta-estimator كطريقة لتقليل التباين في black-box estimator (على سبيل المثال، شجرة القرار)، عن طريق إدخال العشوائية في إجراءات البناء الخاصة به ثم إنشاء مجموعة منه.

from sklearn.ensemble import BaggingClassifier
Model=BaggingClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))

#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

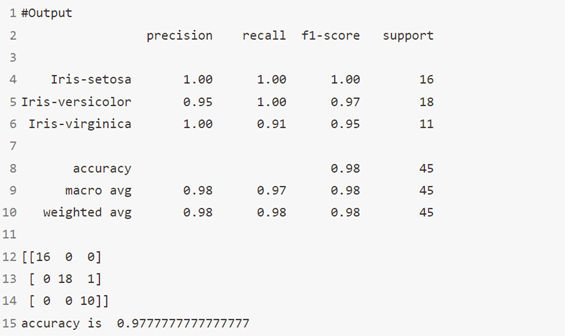
خوارزمية 13: مصنف  AdaBoost

مُصنِّف AdaBoost هو meta-estimator يبدأ بتركيب مُصنِّف على مجموعة البيانات الأصلية ثم يُلائم نُسخًا إضافية من المُصنِّف في نفس مجموعة البيانات ولكن حيث يتم تعديل أوزان الحالات المصنفة بشكل غير صحيح بحيث تركز المصنفات اللاحقة بشكل أكبر على الحالات الصعبة.

from sklearn.ensemble import AdaBoostClassifier
Model=AdaBoostClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

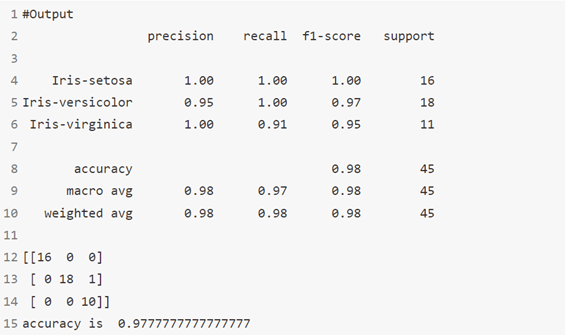
خوارزمية 14: تصنيف تعزيز التدرج Gradient Boosting Classifier

GBM هي خوارزمية تعزيز تُستخدم عندما نتعامل مع الكثير من البيانات لعمل تنبؤ بقوة تنبؤ عالية. التعزيز Boosting هو في الواقع مجموعة من خوارزميات التعلم التي تجمع بين توقع العديد من المخمنات الأساسية من أجل تحسين المتانة على مخمن واحد. فهو يجمع بين عدة متنبئين ضعيفين أو متوسطين لبناء متنبئ قوي.

from sklearn.ensemble import GradientBoostingClassifier
Model=GradientBoostingClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))

#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

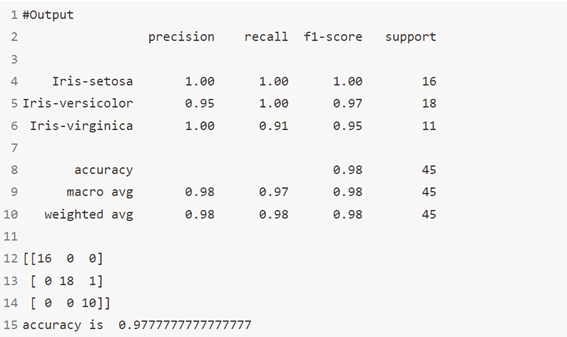
الخوارزمية 15: تحليل التمييز الخطي Linear Discriminant Analysis

المصنف بحد القرار الخطي linear decision boundary، يتم إنشاؤه عن طريق ملاءمة الكثافة الشرطية للفئة للبيانات واستخدام قاعدة بايز Bayes’ rule.

يناسب النموذج كثافة Gaussian لكل فئة، على افتراض أن جميع الفئات تشترك في نفس مصفوفة التغاير covariance matrix.

يمكن أيضًا استخدام النموذج الملائم fitted model لتقليل أبعاد المدخلات من خلال إسقاطه على الاتجاهات الأكثر تمييزًا.

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
Model=LinearDiscriminantAnalysis()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))

#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

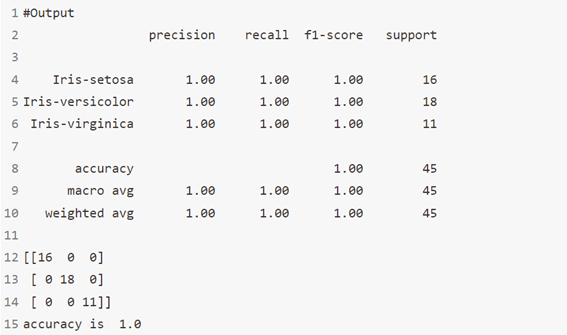
الخوارزمية 16: تحليل التمييز التربيعي Quadratic Discriminant Analysis

مصنف مع حد قرار تربيعي quadratic decision boundary ، يتم إنشاؤه عن طريق ملاءمة الكثافة الشرطية للفئة للبيانات واستخدام قاعدة بايز.

يناسب النموذج كثافة Gaussian لكل فئة.

from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
Model=QuadraticDiscriminantAnalysis()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)

# Summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))

#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))

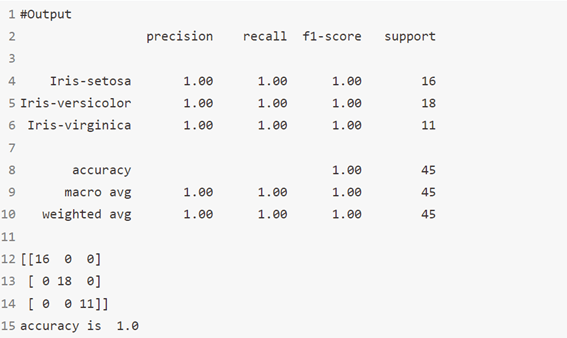
خوارزمية 17: K- means

إنه نوع من الخوارزمية غير الخاضعة للإشراف والتي تحل مشكلة التجميع clustering. يتبع الإجراء طريقة بسيطة وسهلة لتصنيف مجموعة بيانات معينة من خلال عدد معين من المجموعات (افترض k مجموعات). نقاط البيانات داخل الكتلة متجانسة وغير متجانسة لمجموعات النظراء.

تذكر اكتشاف الأشكال من بقع الحبر؟ k يعني أن هذا النشاط مشابه إلى حد ما. تنظر إلى الشكل وتنتشر لفك عدد المجموعات / المجموعات المختلفة الموجودة.

x = data.iloc[:, [1, 2, 3, 4]].values

#Finding the optimum number of clusters for k-means classification
from sklearn.cluster import KMeans
wcss = []

for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 0)
    kmeans.fit(x)
    wcss.append(kmeans.inertia_)
    
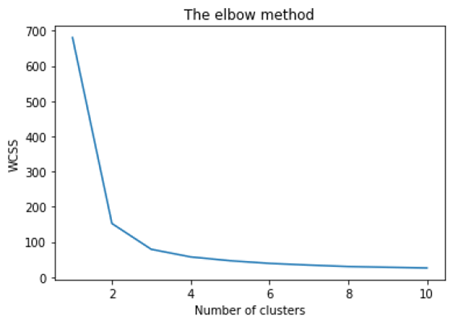
#Plotting the results onto a line graph, allowing us to observe 'The elbow'
plt.plot(range(1, 11), wcss)
plt.title('The elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS') # within cluster sum of squares

#Applying kmeans to the dataset / Creating the kmeans classifier
kmeans = KMeans(n_clusters = 3, init = 'k-means++', max_iter = 300, n_init = 10, random_state = 0)
y_kmeans = kmeans.fit_predict(x)
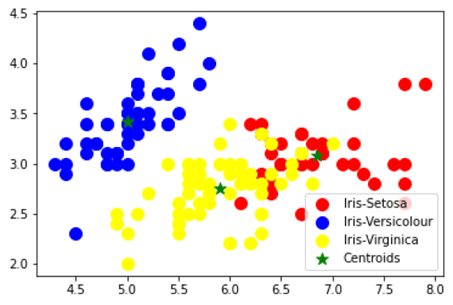
#Visualising the clusters

plt.scatter(x[y_kmeans == 0, 0], x[y_kmeans == 0, 1], s = 100, c = 'red', label = 'Iris-Setosa')
plt.scatter(x[y_kmeans == 1, 0], x[y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Iris-Versicolour')
plt.scatter(x[y_kmeans == 2, 0], x[y_kmeans == 2, 1], s = 100, c = 'yellow', label = 'Iris-Virginica')

#Plotting the centroids of the clusters
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:,1], s = 100, c = 'green', label = 'Centroids',marker='*')

plt.legend()

آمل أن تعجبك هذه المقالة حول جميع خوارزميات التعلم الآلي.