معالجة البيانات غير المتوازنة في التعلم الآلي والتعلم العميق

مقدمة

مشاكل التصنيف Classification problems شائعة جدًا في عالم التعلم الآلي. كما نعلم في مشكلة التصنيف، نحاول التنبؤ بتسمية الفئة من خلال دراسة بيانات الإدخال أو المتنبئ حيث يكون الهدف أو متغير الإخراج متغيرًا فئويًا في الطبيعة.

إذا كنت قد تعاملت بالفعل مع مشاكل التصنيف، فيجب أن تكون قد واجهت حالات يكون فيها عدد ملاحظة أحد تسميات الفئات المستهدفة أقل بكثير من تسميات الفئة الأخرى. يُطلق على هذا النوع من مجموعات البيانات مجموعة بيانات فئة غير متوازنة imbalanced class dataset وهي شائعة جدًا في سيناريوهات التصنيف العملية. غالبًا ما يؤدي أي نهج معتاد لحل هذا النوع من مشكلات التعلم الآلي إلى نتائج غير مناسبة.

في هذه المقالة، سأناقش مجموعة البيانات غير المتوازنة، والمشكلة المتعلقة بالتنبؤ بها، وكيفية التعامل مع هذه البيانات بشكل أكثر كفاءة من الطريقة التقليدية.

ما هي البيانات غير المتوازنة وكيفية التعامل مع مجموعة البيانات غير المتوازنة؟

تشير البيانات غير المتوازنة إلى تلك الأنواع من مجموعات البيانات حيث يكون للفئة المستهدفة توزيع غير متساوٍ للملاحظات، أي أن تصنيف أحد الفئات يحتوي على عدد كبير جدًا من الملاحظات والآخر يحتوي على عدد قليل جدًا من الملاحظات. يمكننا أن نفهم بشكل أفضل التعامل مع مجموعة البيانات غير المتوازنة بمثال.

لنفترض أن XYZ هو بنك يصدر بطاقة ائتمان لعملائه. يشعر البنك الآن بالقلق من استمرار بعض المعاملات الاحتيالية وعندما يتحقق البنك من بياناته، وجد أنه لكل معاملة 2000، تم تسجيل 30 عددًا فقط من عمليات الاحتيال. لذا، فإن عدد عمليات الاحتيال لكل 100 معاملة أقل من 2٪، أو يمكننا القول أن أكثر من 98٪ معاملة “غير احتيالية No Fraud” بطبيعتها. هنا، تسمى فئة “غير الاحتيالية” طبقة الأغلبية majority class، وتسمى فئة “الاحتيال Fraud” الأصغر حجمًا فئة الأقلية minority class.

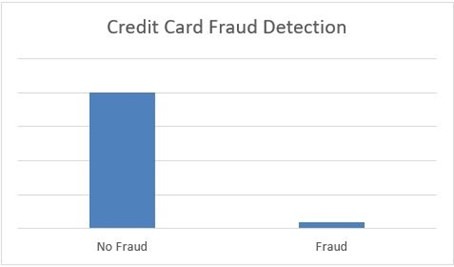
المزيد من الأمثلة على البيانات غير المتوازنة هي :

• تشخيص المرض.
  • توقعات تناقص العملاء.
  • الكشف عن الغش.
  • كارثة طبيعية.

الفئة غير المتوازنة طبيعية بشكل عام في مشاكل التصنيف. ولكن، في بعض الحالات، يكون هذا الخلل حادًا للغاية حيث يكون وجود طبقة الأغلبية أعلى بكثير من طبقة الأقلية.

مشاكل تصنيف البيانات غير المتوازنة

إذا شرحناها بطريقة بسيطة للغاية، فإن المشكلة الرئيسية في التنبؤ غير المتوازن لمجموعة البيانات هي مدى دقة توقعنا في الواقع لفئة الأغلبية والأقلية؟ دعونا نشرحها بمثال لتشخيص المرض. لنفترض أننا سنتوقع المرض من مجموعة بيانات موجودة حيث يتم تشخيص إصابة 5 مرضى فقط بالمرض لكل 100 سجل. لذا، فإن فئة الأغلبية 95٪ بدون مرض وفئة الأقلية 5٪ فقط مصابة بالمرض. الآن، افترض أن نموذجنا يتوقع أن 100 من كل 100 مريض ليس لديهم أي مرض.

في بعض الأحيان عندما تكون سجلات فئة معينة أكثر بكثير من الفئة الأخرى، قد ينحاز المصنف classifier لدينا نحو التنبؤ. في هذه الحالة، توضح مصفوفة الارتباك confusion matrix الخاصة بمشكلة التصنيف مدى جودة تصنيف نموذجنا للفئات المستهدفة ونصل إلى دقة النموذج من مصفوفة الارتباك. يتم حسابه بناءً على العدد الإجمالي للتنبؤات الصحيحة بواسطة النموذج مقسومًا على العدد الإجمالي للتنبؤات. في الحالة أعلاه (0 + 95) / (0 + 95 + 0 + 5) = 0.95 أو 95٪. هذا يعني أن النموذج فشل في تحديد فئة الأقلية ولكن درجة دقة النموذج ستكون 95٪. وبالتالي فإن نهجنا التقليدي في التصنيف وحساب دقة النموذج ليس مفيدًا في حالة مجموعة البيانات غير المتوازنة.

طرق للتعامل مع مشكلة مجموعة البيانات غير المتوازنة

في حالات نادرة مثل اكتشاف الاحتيال أو التنبؤ بالمرض، من الضروري تحديد فئات الأقليات بشكل صحيح. لذلك لا ينبغي أن يكون النموذج متحيزًا لاكتشاف طبقة الأغلبية فقط ولكن يجب أن يعطي وزناً أو أهمية متساوية تجاه طبقة الأقلية أيضًا. أنا هنا أناقش بعض التقنيات القليلة التي يمكن أن تتعامل مع هذه المشكلة. لا توجد طريقة صحيحة أو طريقة خاطئة في هذا، فالتقنيات المختلفة تعمل بشكل جيد مع المشكلات المختلفة.

1. اختر مقياس التقييم المناسب

دقة accuracy المصنف هي العدد الإجمالي للتنبؤات الصحيحة بواسطة المصنف مقسومًا على العدد الإجمالي للتنبؤات. قد يكون هذا جيدًا بما يكفي لفئة متوازنة ولكنه ليس مثاليًا لمشكلة الفئة غير المتوازنة. المقاييس الأخرى مثل الدقة precision هي مقياس مدى دقة تنبؤ المصنف لفئة معينة والاستدعاء recall هو مقياس قدرة المصنف على تحديد فئة.

بالنسبة لمجموعة بيانات الفئة غير المتوازنة، تعد درجة F1 مقياسًا أكثر ملاءمة. إنها المتوسط التوافقي harmonic mean للدقة precision والاستدعاء recall والتعبير هو:

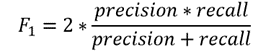
لذلك، إذا توقع المصنف فئة الأقلية ولكن التنبؤ خاطئ وزيادات إيجابية كاذبة، فسيكون مقياس الدقة منخفضًا وكذلك درجة F1. أيضًا، إذا كان المصنف يحدد فئة الأقلية بشكل سيئ، أي أن عددًا أكبر من هذه الفئة تم توقعه بشكل خاطئ على أنه فئة الأغلبية، فستزيد السلبيات الخاطئة، لذلك ستنخفض درجة الاستدعاء وستكون درجة F1 منخفضة. تزيد درجة F1 فقط إذا تحسن كل من عدد وجودة التنبؤ.

تحافظ درجة F1 على التوازن بين الدقة والاستدعاء وتحسن النتيجة فقط إذا حدد المصنف المزيد من فئة معينة بشكل صحيح.

2. إعادة اخذ العينات Resampling (الإفراط في أخذ العينات Oversampling ونقص العينات Undersampling)

تُستخدم هذه التقنية للافراط في اخذ العينات أو تقليص عينات فئة الأقلية أو الأغلبية. عندما نستخدم مجموعة بيانات غير متوازنة، يمكننا زيادة عينة فئة الأقلية باستخدام الاستبدال. هذه التقنية تسمى الإفراط في أخذ العينات oversampling. وبالمثل، يمكننا حذف الصفوف عشوائيًا من فئة الأغلبية لمطابقتها مع فئة الأقلية التي تسمى underampling. بعد أخذ عينات البيانات، يمكننا الحصول على مجموعة بيانات متوازنة لكل من فئات الأغلبية والأقلية. لذلك، عندما يكون لدى كلا الفئتين عدد مماثل من السجلات الموجودة في مجموعة البيانات، يمكننا أن نفترض أن المصنف سيعطي أهمية متساوية لكلا الفئتين.

يتم عرض مثال على هذه التقنية باستخدام مكتبة resample()  من sklearn أدناه لأغراض التوضيح. هنا، Is_Lead هو المتغير المستهدف target لدينا. دعونا نرى توزيع الفئات في الهدف.

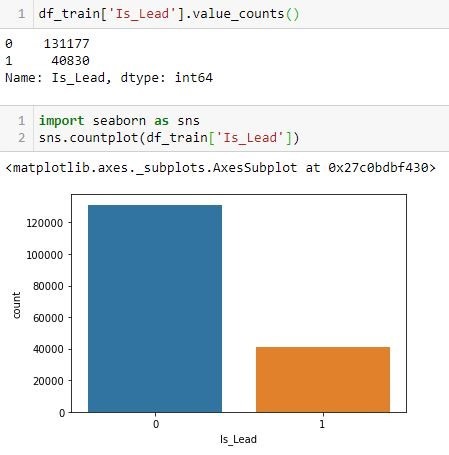
لقد لوحظ أن فئتنا المستهدفة بها خلل. لذلك، سنحاول الافراط في اخذ العينات upsample بحيث تتطابق فئة الأقلية مع فئة الأغلبية.

from sklearn.utils import resample
#create two different dataframe of majority and minority class 
df_majority = df_train[(df_train['Is_Lead']==0)] 
df_minority = df_train[(df_train['Is_Lead']==1)] 
# upsample minority class
df_minority_upsampled = resample(df_minority, 
                                 replace=True,    # sample with replacement
                                 n_samples= 131177, # to match majority class
                                 random_state=42)  # reproducible results
# Combine majority class with upsampled minority class
df_upsampled = pd.concat([df_minority_upsampled, df_majority])

بعد upsampling، يكون توزيع الفئة متوازنًا على النحو التالي:

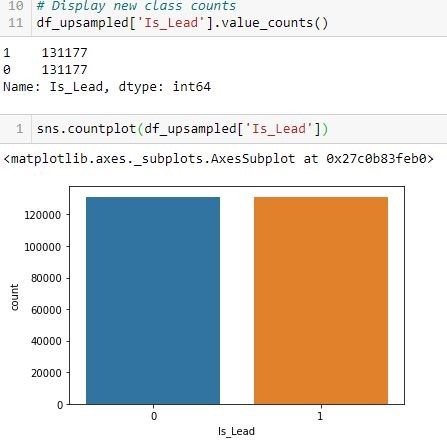
يمكن استخدام Sklearn.utils resample لكل من عينات فئة الأغلبية ومثيلات فئة الأقلية بكميات كبيرة.

3. SMOTE

تعتبر تقنية الإفراط في أخذ عينات الأقليات الاصطناعية Synthetic Minority Oversampling Technique أو SMOTE أسلوبًا آخر للإفراط في أخذ عينة من فئة الأقلية. إن إضافة سجلات مكررة لفئة الأقلية غالبًا لا تضيف أي معلومات جديدة إلى النموذج. في SMOTE يتم تصنيع حالات جديدة من البيانات الموجودة. إذا قمنا بشرحها بكلمات بسيطة، فإن SMOTE تنظر في حالات فئة الأقليات وتستخدم k أقرب جار k nearest neighbor لتحديد أقرب جار عشوائي، ويتم إنشاء مثيل اصطناعي عشوائيًا في مساحة الميزة.

سأقوم بعرض نموذج الكود نفسه أدناه :

from imblearn.over_sampling import SMOTE
# Resampling the minority class. The strategy can be changed as required.
sm = SMOTE(sampling_strategy='minority', random_state=42)
# Fit the model to generate the data.
oversampled_X, oversampled_Y = sm.fit_sample(df_train.drop('Is_Lead', axis=1), df_train['Is_Lead'])
oversampled = pd.concat([pd.DataFrame(oversampled_Y), pd.DataFrame(oversampled_X)], axis=1)

الآن تمت موازنة الفئة على النحو التالي:

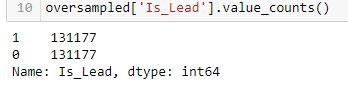
4. BalancedBaggingClassifier

عندما نحاول استخدام المصنف المعتاد لتصنيف مجموعة بيانات غير متوازنة، يفضل النموذج فئة الأغلبية نظرًا لوجودها الأكبر حجمًا. يعتبر BalancedBaggingClassifier هو نفسه مصنف sklearn ولكن مع موازنة إضافية. يتضمن خطوة إضافية لموازنة مجموعة التدريب في وقت الملاءمة لأخذ عينات معين. يأخذ هذا المصنف معلمتين خاصتين ” ampling_strategy” و “replacement”. تحدد إستراتيجية أخذ العينات sampling_strategy نوع إعادة اخذ العينات المطلوبة (على سبيل المثال “الأغلبية” – إعادة أخذ عينة من فئة الأغلبية فقط، “الكل” – إعادة عينة جميع الفئات، إلخ) ويقرر الاستبدال replacement ما إذا كان سيكون عينة مع الاستبدال أم لا.

ويرد مثال توضيحي أدناه:

from imblearn.ensemble import BalancedBaggingClassifier
from sklearn.tree import DecisionTreeClassifier
#Create an instance
classifier = BalancedBaggingClassifier(base_estimator=DecisionTreeClassifier(),
                                sampling_strategy='not majority',
                                replacement=False,
                                random_state=42)
classifier.fit(X_train, y_train)
preds = classifier.predict(X_test)

5. Threshold moving

في حالة المصنفات الخاصة بنا، يتنبأ المصنفون في كثير من الأحيان باحتمالية عضوية الفئة. نقوم بتعيين احتمالات هذا التوقع لفئة معينة بناءً على عتبة تكون عادةً 0.5، أي إذا كانت الاحتمالات <0.5 تنتمي إلى فئة معينة، وإذا لم تكن تنتمي إلى فئة أخرى.

بالنسبة لمشاكل الفئة غير المتوازنة، قد لا يعمل هذا الحد الافتراضي بشكل صحيح. نحن بحاجة إلى تغيير العتبة إلى القيمة المثلى حتى تتمكن من فصل فئتين بكفاءة. يمكننا استخدام منحنيات ROC و Precision-Recall Curves للعثور على الحد الأمثل للمصنف. يمكننا أيضًا استخدام طريقة بحث الشبكة grid search أو البحث ضمن مجموعة من القيم لتحديد القيمة المثلى.

البحث عن القيمة المثلى من الشبكة

في هذه الطريقة أولاً، سنجد الاحتمالات الخاصة بتسمية الفئة، ثم سنجد الحد الأمثل لتعيين الاحتمالات إلى تصنيف الفئة المناسب. يمكن الحصول على احتمالية التنبؤ من المصنف باستخدام  predict_proba()  من sklearn.

from sklearn.ensemble import RandomForestClassifier
rf_model = RandomForestClassifier()
rf_model.fit(X_train,y_train)   
rf_model.predict_proba(X_test) #probability of the class label

المخرجات:

array([[0.97, 0.03],
       [0.94, 0.06],
       [0.78, 0.22],
       ...,
       [0.95, 0.05],
       [0.11, 0.89],
       [0.72, 0.28]])

بعد الحصول على الاحتمال يمكننا التحقق من القيمة المثلى.

step_factor = 0.05 
threshold_value = 0.2 
roc_score=0
predicted_proba = rf_model.predict_proba(X_test) #probability of prediction
while threshold_value <=0.8: #continue to check best threshold upto probability 0.8
    temp_thresh = threshold_value
    predicted = (predicted_proba [:,1] >= temp_thresh).astype('int') #change the class boundary for prediction
    print('Threshold',temp_thresh,'--',roc_auc_score(y_test, predicted))
    if roc_score<roc_auc_score(y_test, predicted): #store the threshold for best classification
        roc_score = roc_auc_score(y_test, predicted)
        thrsh_score = threshold_value
    threshold_value = threshold_value + step_factor
print('---Optimum Threshold ---',thrsh_score,'--ROC--',roc_score)

المخرجات:

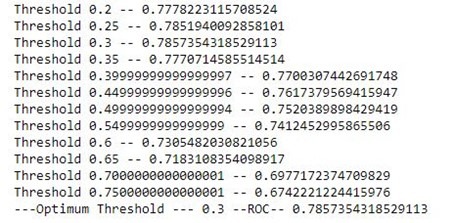
هنا، نحصل على الحد الأمثل عند 0.3 بدلاً من القيمة الافتراضية 0.5.

الاستنتاج:

آمل أن تعطيك هذه المقالة فكرة عن بعض الأساليب التي يمكن استخدامها أثناء التعامل مع مجموعة البيانات غير المتوازنة.